Pendulums are one of the earliest machines we see and Physics courses can take advantage of that familiarity to reveal fundamental principles and demonstrate the mathematical relationships.
In this demonstration, I suspended an NXT with three sensors from above, and let it swing back and forth, recording the data via Bluetooth to the NXT-G data logging window.
The sensors logged were the NXT Ultrasonic sensor, Light sensor, and HiTechnic accelerometer mounted on the bottom of the pendulum. The NXT internal timer was also used to determine sample rate and experiment duration, but that will probably be transparent to most students.
The program was very simple – essentially two data logging blocks:

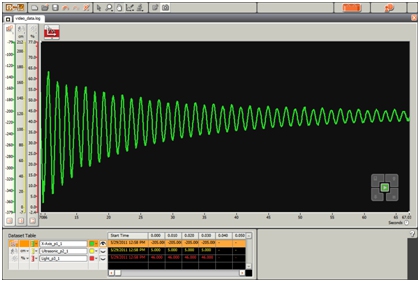
Here’s a snapshot of the resulting accelerometer plot:
Depending on your goals, and the readiness of your students, you can ask them to do a lot of things with this exercise. Some of them include:
- predict the pendulum period
- predict pendulum period variation with length
- determine how pendulum weight affects period (sneaky question – it doesn’t)
- measure acceleration due to gravity
For the elementary kids, don’t think they’re left out. One of the ways to get them thinking about the periodic motion would be to study the relationships of all three data streams and see if they can tell what’s going on in each part.
Here’s an example:
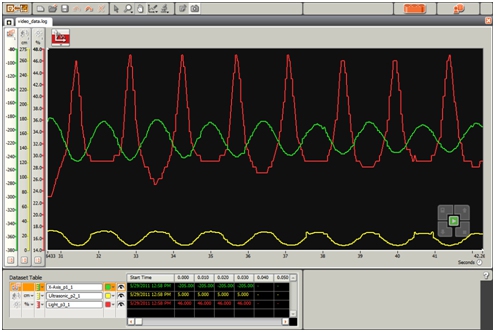
So when the light sensor is reading the brightest, it is closest to the floor, which aligns with the accelerometer showing maximum negative acceleration, and the ultrasonic sensor showing closest proximity to the floor.
The width of the light sensor spike also reveals that the pendulum is moving fastest (narrow peaks of light sensor curve) when it’s closest to the floor (bottom of the swing) and slows down as it nears the top of the swing (widest, lowest points of light sensor curve).
Just having the younger kids walk through these qualitative relationships should help them make connections in other analytic subjects later on.
For kids that are ready for the math, here’s the pendulum equation:
T = 2π√(L/g)
or
Period (time) = 2π* Square Root of (pendulum Length/acceleration due to gravity)
For students ready to embark on differential equations or signal processing, this should be a decent challenge to predict or develop the equation for the exponentially damped sinusoid curve that’s shown in the logged data.
Further Extension For Any Age Students
In the images above you’ll see I chose 100 samples per second (100 Hz) for my sample rate. For the hot runner students who get done and start being bored (or the mathematicians) ask the students to start lowering the sample rate and observe the effects on the logged curve. If time is short, tell them to pick a sample rate that’s close to the pendulum’s period. Then ask them why the logged data doesn’t look like their earlier curve with the higher sample rate. If they used their pendulum’s period, the logged data should be a flat line.
What’s going on?
Too low a sample rate violates the Nyquist Theorem, or Sampling Theorem which tells us that any sampled signal must be sampled at least twice as fast as its highest frequency. This is why compact disk music is sampled at 44,100 Hz, because humans can only hear up to about 20,000 Hz.
Pitfalls
At first blush, you might think hanging the NXT Intelligent Brick on a string would be sufficient, but unfortunately it tends to spin, which disturbs the signals and the data being collected. To prevent this, the intelligent brick needs to be constrained such that it can swing only about one axis. I used an arrangement of studless beams and an axle to make that happen.
Watch the NXT Ultrasonic sensor – if it does not get a return, it defaults to a value of 255 cm or 100 inches, which has a tendency to foul up the ultrasonic curve early in the experiment.
Further reading
- Physics with Robotics: An NXT and RCX Activity Guide for Secondary and College Physics. William Church, Tony Ford, Natasha Perova – activities for this post derived from Exercise 4.6 Swinging with Gravity pages 90 – 92, but adapted for NXT-G data logging. Available direct from the publisher College House Books (compare prices)
- Wikipedia: Damped Sine Wave
- Wikipedia: Pendulum
- Wikipedia: Sampling Theorem
- Powerpoint file showing more details.
- This post as a MS Word file
Latest posts by Craig (see all)
- NXT exercises – One approach - 2 February 2016
- Why I like educational robots - 18 November 2013
- Area Measurement: Follow the Path - 27 May 2013
- Program structure – simulating publish and subscribe - 25 May 2013
- Pendulum mathematics - 25 May 2013